Complex Arithmetic

Samples - Polar

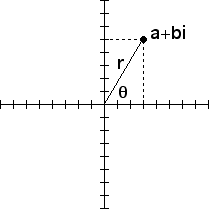
Complex numbers also can be represented using polar coordinates. From the picture, it is easy to see that

r = sqrt(a² + b²) = |a + bi|

tan(theta) = b/a, theta is called the argument of the complex number

a = rcos(theta)

b = rsin(theta)

Addition of complex numbers has a simple interpretation using cartesian coordinates. We shall see multiplication has a simple interpretation using polar coordinates.

Suppose a + bi has polar representation (r, theta) and c + di has polar representation (s, phi).

The modulus of the product of two complex numbers is the product of their moduli:

|a + bi|*|c + di| = |(a + bi)*(c + di)|

Here is why.

(a + bi)*(c + di) = (ac - bd) + (ad + bc)i

so |(a + bi)*(c + di)| = sqrt[(ac - bd)2 + (ad + bc)2]

= sqrt[a2c2 - 2abcd + b2d2 + a2d2 + 2abcd + b2c2]

= sqrt[a2c2 + b2d2 + a2d2 + b2c2]

= sqrt[a2(c2 + d2) + b2(c2 + d2)]

= sqrt[a2 + b2]*sqrt[c2 + d2]

= |a + bi|*|c + di|

Finally, the argument of the sum of two complex numbers is the sum of their arguments.

Here is why.

Suppose gamma is the argument of (a + bi)*(c + di)

Then tan(gamma) = (ad + bc)/(ac - bd)

Recall tan(theta + phi) = (tan(theta) + tan(phi))/(1 - tan(theta)*tan(phi))

So tan(theta + phi) = ((b/a) + (d/c))/(1 - (b/a)*(d/c))

= (ad + bc)/(ac - bd)

Being careful with signs, we see gamma = theta + phi.

Summarizing:

To multiply two complex numbers, multiply the moduli and add the arguments.

Return to Samples.