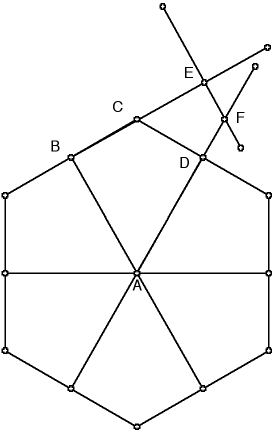
| These side bisectors divide the hexagon into six congruent quadrilaterals called kites. |
| We will construct a kite similar to ABCD but having long side equal to CD. |
| To do this, extend segments BC and AD away from B and A, respectively. |
| On the extended BC, mark point E so that |
| From E, draw a perpendicular to BE until it intersects the extended AD. |
| Label this point of intersection F. |
| The kite ABCD is similar to the kite CEFD because |