Simple Fractal Tilings

Method 2

In method 1 we observe the central region grows more rapidly than the boundary undulations.

To remove this effect, in the second method all parts grow at the same rate.

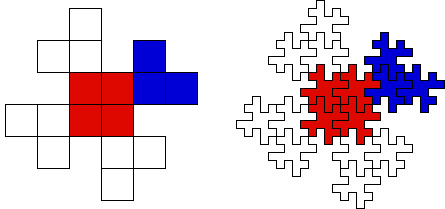
For comparison we will work with the shape of the previous example, but now we will think of the shape divided into subsquares, as seen on the left.

We use the shape divided into subsquares as a blueprint and follow its pattern replacing each subsquare with a suitably reduced original shape.

First notice the center of the shape consists of four subsquares, each of which is replaced by a reduced copy of the shape.

Next, each of the four arms consists of three subsquares, each of which is replaced by a reduced copy of the shape.

These 16 reduced copies of the shape are grouped to form a single object, and the process is iterated using this object.

The original shape tiles the plane, so also will each iterate, being made up of ever smaller copies of the original tile.

To see the limiting tile has a fractal boundary, recall the area-perimeter relationship, by which we found the limiting curve has dimension d = 3/2.

Recall starting with the same tile, method 1 produced a tile with boundary curve of dimension d = 1.36521. So even when we start with the same pattern, methods 1 and 2 can give rise to different fractal tiles.

Must this always be so? Are there configurations for which both methods give rise to the same tile?

A variation on this process could have given Escher an intersting idea.

Return to Simple Fractal Tiles.