Visualizing Iteration Patterns

Exercises

1. In this exercise we explore some relations between the behavior of the logistic map L(x) and its iterate L2(x) = L(L(x)). We shall use the graphical iteration and the histogram windows.

(a) To review the behavior of the logistic map, find s values for which the map has a stable fixed point, stable 2-cycle, and stable 4-cycle. Write the s-value and sketch the graphical iteration window.

s = s = s = fixed point 2-cycle 4-cycle

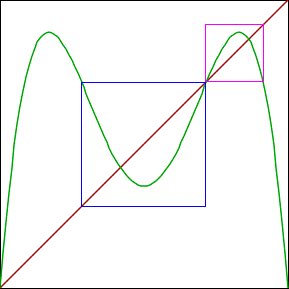
Adjust the composition to 2 and the s-value to about 3.55. Superimposed on the graph of L2 are two squares, denoted the central square and the right square.

(b) Adjust the s value so the iterates of an initial point in the central square converge to a fixed point in the central square, and the iterates of an initial point in the right square converge to a fixed point in the right square. Recall initial points can be selected by mouse clicks. Record the s-value. Here is the answer.

(c) Adjust the s value so the iterates of an initial point in the central square converge to a 2-cycle in the central square, and the iterates of an initial point in the right square converge to a 2-cycle in the right square. Record the s-value. Here is the answer.

(d) Adjust the s value so the iterates of an initial point in the central square converge to a 4-cycle in the central square, and the iterates of an initial point in the right square converge to a 4-cycle in the right square. Record the s-value. Here is the answer.

(e) Adjust the composition back to 1. What cycle for L(x) corresponds to each of the L2 cycles of parts (b), (c), and (d)? Comment on the relations between these cycles for L(x) and those for L2(x). Here is an answer.

(b) For this s-value, do the L-iterates of a point appear chaotic? Here is an answer.

2. (a) Find an s-value for which the iterates under L2 of a point in the central square appear chaotic, but stay within that square. For this s-value, what happens to iterates of a point in the right square? Here is an answer.

(c) Find an s-value for which the iterates of a point in the central square escape from that square. For this s-value, what happens to iterates of points in the right square? Explain this behavior in terms of the relation between the central and right squares and the graph of L2(x). Here is an answer.

(d) Use the bifurcation diagram to approximate the s-value at which the iterates of L2 begin to escape from the central and the right squares. Here is an answer.

(e) Look again at the bifurcation diagam and describe how the dynamics of the iterates of L2 in the central or the right square are related to the iterates of L. Here is an answer.

Return to Visualizing Iteration Patterns.