 |
| r | s | theta |
phi | e | f |
| 1 | 0.5 | 0.5 | 0 |
0 | 0 | 0 |
| 2 | 0.5 | 0.5 | 0 |
0 | 0.5 | 0.5 |
| 3 | 0.25 | 0.25 | 0 |
0 | 0.5 | 0 |
| 4 | 0.25 | 0.25 | 0 |
0 | 0.75 | 0.25 |
| 5 | 0.25 | 0.25 | 0 |
0 | 0 | 0.5 |
| 6 | 0.25 | 0.25 | 0 |
0 | 0.25 | 0.75 |
| 7 | 0.125 | 0.125 | 0 |
0 | 0.25 | 0.5 |
| 8 | 0.125 | 0.125 | 0 |
0 | 0.375 | 0.625 |
|
 |
|
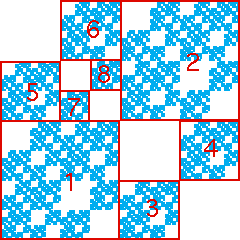
| Here are the IFS rules to generate this picture. Denote the whole picture by A. |
| Click each part of A to see the sequence of edges of the graph that generate that part. |
| Note the subsquares with addresses 1 and 4 are romes. So for example |
| T1(A) = T1(T1(A) ∪
T2(A) ∪ T3(A) ∪
T4(A)) |
| because each of the transitions 1 → 1, 1 → 2, 1 → 3, and
1 → 4 is allowed. |
| That is, the subsquare with address 1 contains a copy of A scaled by 1/2. |
| Similarly, the subsquare with address 4 contains a copy of A scaled by 1/2. |
| Because 2 and 3 are not romes, those subsquares do not contain copies of A scaled by 1/2. |
| Because 1 → 2 and 4 → 2 are the only transitions into subsquare 2, that
square contains two copies of A, |
T2(T1(A)) and T2(T4(A)), both scaled
by a factor of 1/4. |
| Finally, the transitions 1 → 3, 4 → 3, and 2 → 3
are allowed, so subsquare 3 contains four copies of A |
T3(T1(A)) and T3(T4(A)), both scaled
by a factor of 1/4, and T3(T2(T1(A))) and
T3(T2(T4(A))), both scaled
by a factor of 1/8. |

