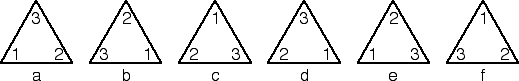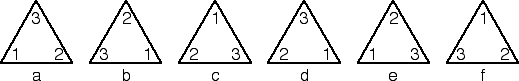| 2. Place (1,0) in all the boxes on the left side of the triangle template,
and (0,1) in all the boxes on the right side. Fill in the rest of the triangle using
the group table. |
Shade the boxes containing (0,0). |
Shade the boxes containing (1,0). |
Shade the boxes containing (0,1). |
Shade the boxes containing (1,1). |
Shade the boxes containing (0,0) or (1,0). |
Shade the boxes containing (0,1) or (1,1). |
Shade the boxes containing (0,0) or (0,1). |
Shade the boxes containing (1,0) or (1,1). |
Repeat this exercise putting different elements along the left and
right edges. What patterns do you see? |
Answer |
| 4. Generate the Pascal's triangle placing b along the left side and d
along the right side. |
Shade all boxes containing a, b, or c. |
Now shade all boxes containing d, e, or f. |
Shade all the boxes containing
d, e, or f for the Pascal's triangle with b along the left side and e along
the right, and with b along the left side and f along the right. |
| Explain the pattern you will get shading a, b, and c if the
triangle is generated by b and c, if the triangle is generated by d and e. |
| In the Pascal's triangle for Z6 we found patterns found in the
Pascal's triangle for Z2 and for Z3. |
| In D3 we find a Pascal's triangle found in Z2.
Can you find a Pascal's triangle found intfound in Z3? |
| Answer |