Basin of Attraction Example

To illustrate finding the basins of attraction, we consider the real version of the first problem Cayley solved for the complex Newton's method.

The function f(x) = x² - 1 has two roots, x = 1 and x = -1. We find the basin of attraction of Newton's method for each root.

graph of the function Take x0 > 1 Take x0 = 1 Take 1 > x0 > 0 Take x0 = 0 Take -1 < x0 < 0 Take x0 = -1 Take x0 < -1

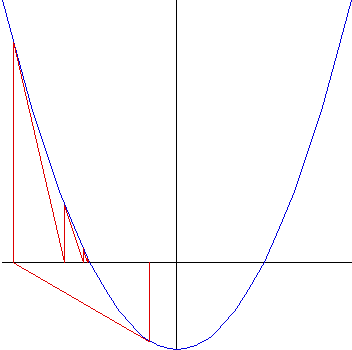Starting with -1 < x0 < 0, we see one iterate of Newton's method gives x1 < -1. From there the points converge to -1. So the basin of attraction of x = -1 includes all x0 satisfying -1 < x0 < 0.

Consequently,

the basin of attraction of x = 1 is all x₀ > 0,

and the basin of attraction of x = -1 is all x₀ < 0.

Return to Complex Newton's Method.