| Take q = 1. Recalling p1 + ... + pN = 1, we see the relation |
| (p1q)(r1tau(q)) + ...
+ (pNq)(rNtau(q)) = 1 |
| that defines tau(q) implies tau(1) = 0 because tau(1) = 0
is a solution of |
| (p11)(r1tau(1)) + ...
+ (pN1)(rNtau(1)) = 1 |
| and for each q the defining equation has
a unique solution. |
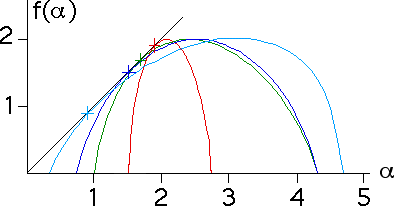
| From the equation f(alpha) = q*alpha + tau(q) we see q = 1
implies f(alpha) = alpha, that is |
| the graph of f(alpha) intersects the diagonal line. |
| Because df/dalpha = q, the diagonal
line is tangent to the graph of f(alpha) at q = 1. |
| Because the graph of f(alpha) is concave down,
this is the only point at which the graph of f(alpha) intersects the diagonal line. |
| Here are some examples for several f(alpha) curves. |
 |

