Random Fractals and the Stock Market

Unifractal Cartoons - the Scaling Condition

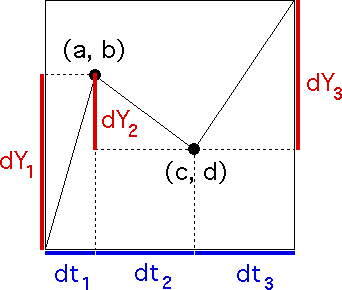
Constructing unifractal cartoons is not difficult, but it does require one bit of care.

The generator starts at (0,0) and ends at (1,1), so the dti and the dYi must satisfy these relations:

dt1 + dt2 + dt3 = 1     (a)

dY1 + dY2 + dY3 = 1     (b)

If we also impose the unifractal scaling condition

|dYi| = (dti)H

and take into account that the generator segments should go up, then down, then up, relation (b) becomes

(dt1)H - (dt2)H + (dt3)H = 1     (c)

Finally, solving relation (a) for dt3 and substituting into (c) gives the unifractal scaling condition

(dt1)H - (dt2)H + (1 - dt1 - dt2)H = 1

Once we specify the coarse Holder exponent H and the interval dt1, only one value of dt2 satisfies the scaling condition.

Moreover, the scaling condition requires 0 < H < 1.

Return to Unifractal Cartoons.