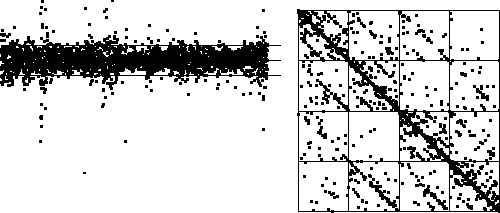
| This is differences of daily closings for the Frankfurt DAX, from 6 Jan, 1986, to
31 Dec, 1997. Updating the dat a dcade or so might show some interesting behavior. |
| The middle bin boundary B2 is taken to be the mean of the
differences, and B1 and B3 are taken 1.5 standard deviations below and
above the mean. |
 |
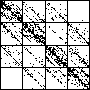
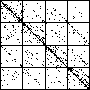
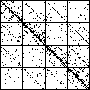
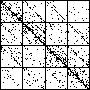
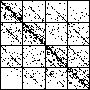
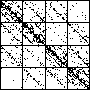
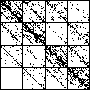
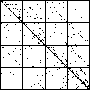
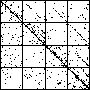
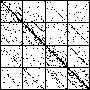
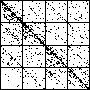
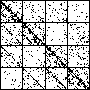
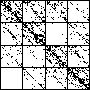
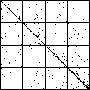
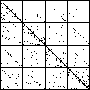
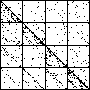
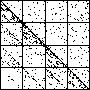
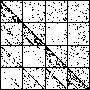
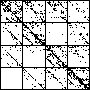
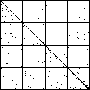
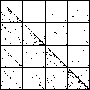
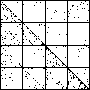
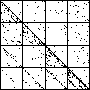
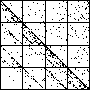
| A natural, and possibly important, problem is to find the cartoon that most closely matches the
data set. |
| For convenience, we shall restrict our attention to
symmetric cartoons,
cartoons whose generators have
turning points (a,b) and (1-a,1-b). |
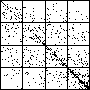
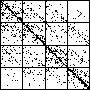
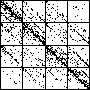
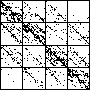
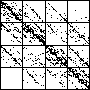
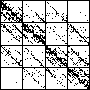
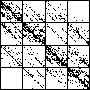
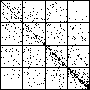
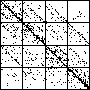
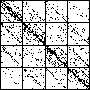
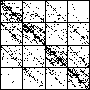
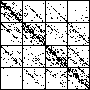
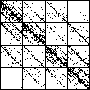
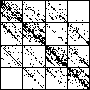
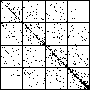
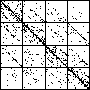
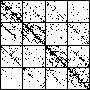
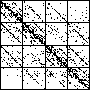
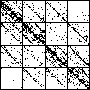
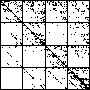
| The chart shows an example of an IFS driven by the differences of the same number of data points as
the DAX data, with the middle bin boundary B2 is taken to be the mean of the
differences, and B1 and B3 are taken 1.5 standard deviations below and
above the mean, for 49 choices of generator. |
| See how well you can match the data to a cartoon.
Click on each picture for an enlargement, in a new window, along with a picture of the generator. |
| Recall these are single
instances and so some details are doubtless influenced by the particular random number sequence used
in creating the cartoon. |
| |
x=0.1 |
x=0.15 |
x=0.2 |
x=0.25 |
x=0.3 |
x=0.35 |
x=0.4 |
| y=0.9 |
 |
 |
 |
 |
 |
 |
 |
| y=0.85 |
 |
 |
 |
 |
 |
 |
 |
| y=0.8 |
 |
 |
 |
 |
 |
 |
 |
| y=0.75 |
 |
 |
 |
 |
 |
 |
 |
| y=0.7 |
 |
 |
 |
 |
 |
 |
 |
| y=0.65 |
 |
 |
 |
 |
 |
 |
 |
| y=0.6 |
 |
 |
 |
 |
 |
 |
 |
|
| Visual comparison is a first step, but it is not the last step in matching cartoons to data.
More analytical methods are under investigation. |


















































