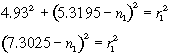First, we have to find the radius of the central circle. Let's plug it in a Cartesian coordinate system and mark line ab as the x-axis and line c0c as the y-axis (Fig.3). c0 is then the origin with coordinates [0;0]. Point c, which lies on the circle has coordinates [0;2] (vaulting rise - 2e). Vaulting span is 10.2e, so points a and b (which also lie on the circle) have coordinates [-5.1;0] and [5.1;0] respectively. According to analytic geometry, the equation of the circle is (x-m)2 + (y-n)2 = r2 where r is the radius of the circle with center C [m;n]. As C should have the same distance from both points a and b, it should lie on the y-axes and thus m = 0. Since we know, that points b and c1 both lie on the curve, we can plug their coordinates into the equation x2 + (y-n)2 = r2:

Point c1: 02 + (2-n)2 = r2 (1)

Point b: 5.12 + (0-n)2 = r2 (2)

From (1) and (2):

4 - 4n' + n2 = 26.01 + n2

n = -5.5025

Since the values on both sides of equation (1) should be positive, we can write:

r = 2 - n = 2 - (-5.5025) = 7.5025

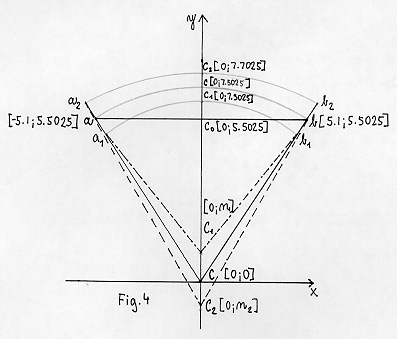
Let's now put the center of the central LINE to the origin of the coordinate system (thus with coordinates C [0;0]) and the line Cc as the x-axis (Fig.4). Thus the coordinates of point c would be xc=0 (as it lies on line x=0) and yc=7.5025 (the radius of the circle is now equal to its distance from the origin). Now we can easily find the coordinate of four other points: c2 [0;7.7025 (the y-coordinate equals the yc plus half of the crown-thickness: y = 7.5025 + 0.4/2)], c1 [0;7.3025 (= 7.5025 - 0.4/2)], c0 [0;5.5025 (=7.5025 - 2, which is the central line rise)], a [-5.1 (half of the vaulting span);5. 5025], b [5.1;5.5025]. Now we have to find the coordinates of a1, b1, a2, and b2. b2: We need to add two lines - one passes through point b and is parallel to the y-axis and the other one passes through b2 and it is parallel to the y-axis. We will mark their intersection B. Since lines Cc0 and bB, Cb and bb2, bc0 and b2B are parallel, the two triangles, Cbc0 and bb2B are similar. Thus:

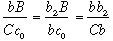
As we know that |bc0| = 5.1, |c0C| = 5.5025, |Cb| = 7.5025 and |bb2| = 0.25 (half of the thickness in the impost), we can easily evaluate the other two:

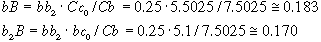
The coordinates of point b2 equals the coordinates of point b plus the (vertical or horizontal) distance of these two points. So we have point b2 [5.6855 (= 5.5025 + 0.183); 5.27 (5.1 + 0.170)]. Since the distance (bb1( equals the distance (bb2( and all three points lie on the same line, the horizontal distances of bb1 and bb2 are also equal - and the same with the vertical distances. So we have the point b1[4.93;5.3195].

Since we can obtain the other half of the figure by simply rotating the construction on the y-axis, the x-coordinates of points a1 and a2 have the same absolute value as b1 and b2 respectively - but they are negative. The y-coordinates are the same.

The equation of the central LINE (let's mark it k) is:

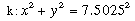
Since its radius is 7.5025 (as we proved before) and the center is at the origin. If we use the same algorithm we used for deriving this equation to derive the equations of circles k1 (which the points a1, b1 and c1 lie on) and k2 (which the points a2, b2 and c2 lie on), we obtain:

where n1 is the y-coordinate of C1 (center of k1) and n2 is the y-coordinate of C2 (center of k2). Thus, r1 = 7.1195, r2 = 7.8935 and the coordinates are C1 [0;0.183] and C2 [0;-0.191].

So the equations are:

Back to the Vaulting A