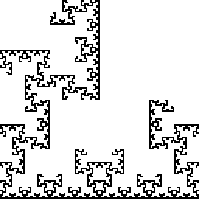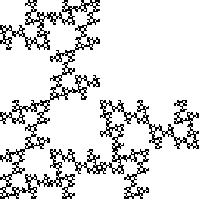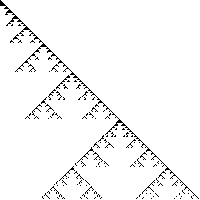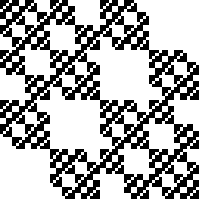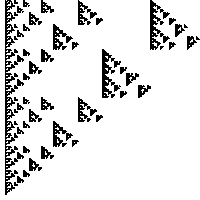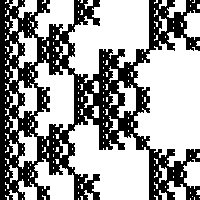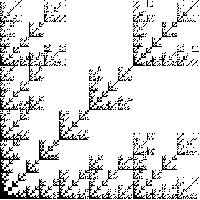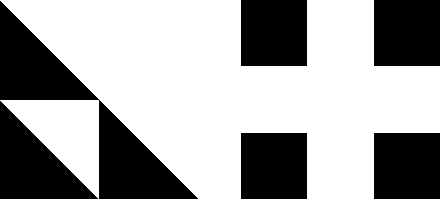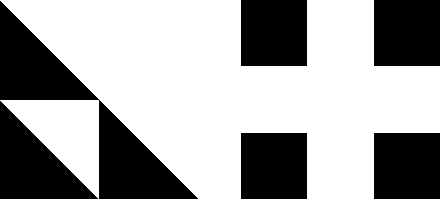Fourth Homework Set Practice

1. Compute the similarity dimensions of these fractals. If you use the similarity dimension formula, list the values of N and of r. If you use the Moran formula, list each of the scaling factors, ri. Solve the Moran formula algebraically (quadratic formula) if possible; otherwise solve it numerically. Present numerical solutions with two digits to the right of the decimal. Click each image for the solution.

(a) (b) (c)   (d) 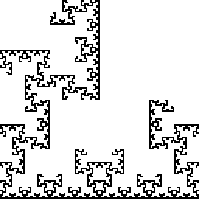(e) (f)   (g) 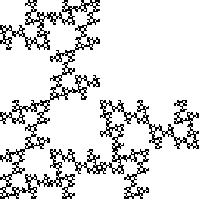(h) 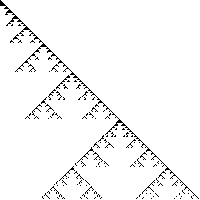(i)  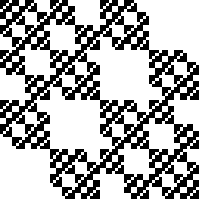 (j) (k) (l) (m) (n) 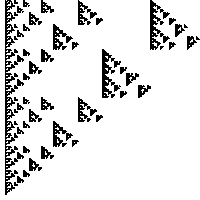(o) 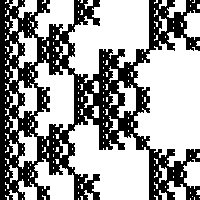(p) 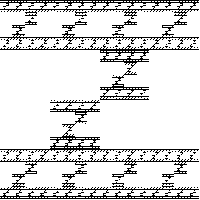(q) (r)

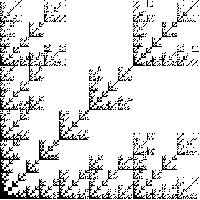2. Pictured below are the first stage images of the construction of the gasket and the product of two Cantor sets.

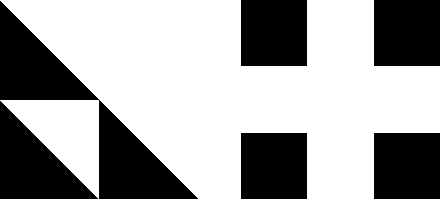(a) Sketch the first stage of the construction fo a fractal having similarity dimension log(5)/log(3).

(b) Sketch the first stage of the construction fo a fractal having similarity dimension log(5)/log(2).Here is the solution.

3. A self-similar fractal in the plane is made of one piece scaled by a factor r = 1/2 and N pieces scaled by a factor r = 1/4.

In this problem, use the Moran formula to find an algebraic (not numerical) expression for the dimension of these fractals.

(a) Find the dimension for the fractal with N = 1.

(b) Find the dimension for the fractal with N = 2.

(c) Find a general expression for the dimension for all N. Your answer should include N.

(d) Find the largest possible value of N. Hint: what is the largest dimension of a shape lying in the plane? Here is the solution.

4. (a) What has the larger dimension, the union of a Sierpinski gasket and a Cantor middle thirds set, or the product of two Cantor middle thirds sets? Explain how you arrived at your answer.

(b) Find the smallest (integer) dimension of the space in which two Sierpinski gaskets typically do not intersect. Hint: compute the dimension of the intersection in dimension 2, 3, etc. Here is the solution.

5. Consider these three shapes

A = Sierpinski gasket, B = Cantor middle-thirds set, C = filled-in unit square

Note dim(A) = Log(3)/Log(2) = 1.585, dim(B) = Log(2)/Log(3) = 0.631, and dim(C) = 2.

Use the appropriate algebra of dimension formulas to compute the dimension of

(a) the union of A and B

(b) the union of B and C

(c) the product of A and B

(d) the product of B and C

(e) the intersection of A and C. Assume both are in 3-dimensional space.

(f) the intersection of B and C. Assume both are in 3-dimensional space.

For each calculation, state which formula you are using and show your calculations.

Here is the solution.

6. (a) Let A denote the Cantor middle-thirds set. Find a fractal (giving the number of pieces and the scaling factors suffices) C for which the union A ∪ C has dimension 1. Explain how you arrived at your answer.

(b) Let A denote the Cantor middle-thirds set situated in 3-dimensional space. Find a fractal D for which the intersection of A and D has dimension 1, or explain why there can be no such set.

(c) Let A denote the Cantor middle-thirds set. Find a fractal (giving the number of pieces and the scaling factors suffices - this will require some thought) B for which the product A × B has dimension 1. Explain how you arrived at your answer.

Here is the solution.

7. Now suppose A is a Sierpinski gasket and B is a Cantor set, but not necessarily the middle-thirds Cantor set. Both are in 2-dimensional space. We know dim(A) = Log(3)/Log(2), but about B all we know is dim(B) < 1.

What is the smallest value of dim(B) for which we expect A and B to have a non-empty intersection?

Hint: recall that if dim(A intersect B) < 0, then typically A and B do not intersect. If dim(A intersect B) = 0, then typically A and B intersect in isolated points. Here is the solution.

8. Compute the box-counting dimension of this shape, a right isosceles Sierpinski gasket, together with a filled-in square.

Do this first by filling in this table. Select values of r appropriate for the scaling symmetry of the shape.

r = square side length N(r) = number of squares   Log(1/r)     Log(N(r))   1 2 0 0.301

Plot the points. Use this information to estimate the box-counting dimension. Do the points appear to lie along a straight line? Do different pairs of points give different slopes?

Modify the argument for computing the box-counting dimension of a gasket together with a line segment to find the box-counting dimension of the shape of problem 2. Comment on the difference between this value and the calculations above. Here is the solution.

9. Find the similarity dimension of a fractal that consists of 2 copies scaled by 1/2, 4 copies scaled by 1/4, and 1 copy scaled by 1/8. Hint: Here the Moran equation is a cubic equation. Move all terms to the same side of the equation, obtaining an expression of the form p(x) = 0, where p(x) is a cubic polynomial. Now x + 1 is a factor of p(x). Divide p(x) by x + 1, obtaining a quadratic polynomial. Apply the quadratic equation to that. If you've forgotten how to divide one polynomial by another, google "dividing polynomials." Here is the solution.

10. (a) Let G denote the Sierpinski gasket in the xy-plane, and let C denote the Cantor middle-thirds set on the z-axis. Find the similarity dimension of the product G × C. Is the dimension > 2 or < 2?

(b) Denote by C(r) the Cantor set consisting of N = 2 pieces, both scaled by r. Find an expression, NOT a numerical value, of r for which G × C(r) has dimension 2. Explain how you arrived at your answer. Hint: remember, Log(r) = a means r = 10a. Here is the solution.

11. Suppose C is a Cantor set consisting of N = 2 pieces, each scaled by a factor of r, and for which dim(C × C × C) = 1. Find r. Here is the solution.

12. Suppose a fractal consists of 3 pieces scaled by 1/2, and 2 pieces scaled by 1/2i for i = 2, 3, 4, ... .

(a) Assuming the Moran equation can be generalized to an infinite collection of transformations (it can) write the Moran equation to find the dimension of this fractal.

(b) Using the fact that

1 + r + r2 + r3 + r4 + ... = 1/(1 - r)

so long as |r| < 1, solve the equation of part (a). Find the dimension of this fractal. Hint: be careful to use the right solution of the quadratic equation. Here is the solution.