Fifth Homework Set Answers

5. (a) The highest probability length N address squares occur where every probability factor is 0.3, so the highest probability is 0.3N.

(b) The corresponding α value is Log(0.3N)/Log(0.5N) = (N Log(0.3))/(N Log(0.5)) = Log(0.3)/Log(0.5) = 1.73697.

(c) The set of points having this α value is the set of points having addresses not containing a 4, that is, the gasket determined by transformations 1, 2, and 3.

(d) The lowest probability length N address squares occur where every probability factor is 0.1, so the highest probability is 0.1N.

(e) The corresponding α value is Log(0.1N)/Log(0.5N) = (N Log(0.1))/(N Log(0.5)) = Log(0.1)/Log(0.5) = 3.32193.

(f) The set of all points having this α value is the set of points having addresses containing only 4s, that is, a single point.

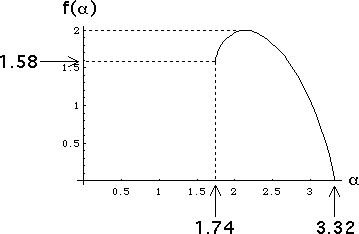
(g) Here is a sketch of the f(α) curve.

The minimum and maximum values of α, approximately 1.74 and 3.32, were computed in (b) and (e).

In (c) we saw that for the minimum value αmin, the set Eαmin is a gasket, hence

f(αmin) = dim(Eαmin) = Log(3)/Log(2), approximately 1.58.

In (f) we saw that for the maximum value of αmax, the set Eαmax is a point, hence

f(αmax) = dim(Eαmax) = 0.

Finally, the maximum value of f(α) is 2, because the four transformations generate a filled-in square.

Return to Homework 5 Practice.