Fifth Homework Set Answers

6. (a) Say the common value of p1, ..., pN is p. Then the condition p1 + ... + pN = 1 becomes Np = 1, or p = 1/N.

(b) In the equation

τ(q) = -Log(p1q + p2q + ... + pNq) / Log(r)

taking p1 = ... = pN = p yields

τ(q) = -Log(N pq) / Log(r)

Using p = 1/N this gives

τ(q) = -Log(N (1/N)q) / Log(r) = -Log(N1-q) / Log(r) = (q - 1)Log(N)/Log(r)

(c) In the equation

α(q) = (p1qLog(p1) + ... + pNqLog(pN)) / (Log(r) (p1q + ... + pNq))

taking p1 = ... = pN = p yields

α(q) = (NpqLog(p)) / (Log(r) N pq) = Log(p) / Log(r)

Note this is independent of q. Using p = 1/N this gives

α(q) = Log(1/N) / Log(r) = Log(N) / Log(1/r)

That is, for each q, α(q) = Log(N) / Log(1/r), the similarity dimension.

(d) From the equation

f(α(q)) = q⋅α(q) + τ(q)

we see

f(α(q)) = (q Log(N)/Log(1/r)) + ((1 - q)Log(N)/Log(1/r)) = Log(N)/Log(1/r)

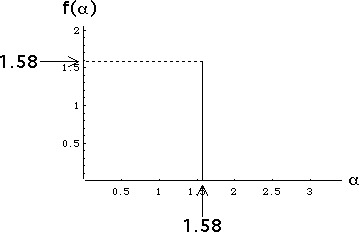
(e) Here is the graph. From (c) we see αmin = αmax = Log(3)/Log(2).

The maximum height of the f(α) curve is the dimension of the attractor, the gasket.

Return to Homework 5 Practice.