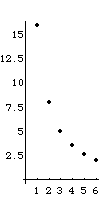Block Fractals

Sample - Area

Here we compute the surface areas of levels 1, 2, and 3, and the surface area of the limiting shape.

Some of the faces of the cubes overlap and some are interior to the shape, so a bit of care is needed with this calculation.

Click the Total Surface Area entry for an explanation of the overlaps.

Level 1	Level 2	Level 3

Level Side Length Number of Cubes Cube Surface Area Total Surface Area 1 1 3 6 A1 = 3*6*1 - 4*1 2 1/2 32 6*((1/2)2) = 6/4 A2 = 3*(3*6*(1/4) - 4*(1/4)) - 4*(1/4) = 6*32*(1/4) - 4*(1/4)*(1 + 3) 3 1/4 33 6*((1/4)2) = 6/(42) A3 = 3*(3*(3*6*(1/4)2 - 4*(1/4)2) - 4*(1/4)2) - 4*(1/4)2 = 6*33*(1/4)2 - 4*(1/4)2*(1 + 3 + 32) ... ... ... ... ... n 1/2n-1 3n 6*((1/2n-1)2) = 6/(4n-1) An = 6*3n*(1/4)n-1 - 4*(1/4)n-1*(1 + 3 + 32 + ... + 3n-1)
		Total Surface Area vs level

Recognizing the bracketed sum in An as a finite geometric series, we see

An = 6*3n*(1/4)n-1 - 4*(1/4)n-1*(1 + 3 + 32 + ... + 3n-1)

= 6*3n*(1/4)n-1 - 4*(1/4)n-1*((1 - 3n)/(1 - 3))

= 12*(3/4)n-1 + 2*(1/4)n-1 - 6*(3/4)n-1

= 6*(3/4)n-1 + 2*(1/4)n-1

So An -> 0 as n -> infinity.

Consequently, the limiting shape has zero area.

This is no surprise: the limiting shape is a right isosceles gasket, having dimension Log(3)/Log(2) < 2.

Area is a 2-dimensional measure, so the area of a Log(3)/Log(2)-dimensional object is 0.

Return to sample.