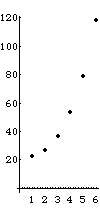Block Fractals

Sample - Perimeter

Here we compute the perimeters (lengths of the edges) of levels 1, 2, and 3, and the perimeter of the limiting shape.

Some of the edges of the cubes are shared between two or three cubes, so a bit of care is needed with this calculation.

Click the Total Perimeter entry for an explanation of the overlaps.

Level 1 Level 2 Level 3

Level Side Length Number of Cubes Cube Perimeter Total Perimeter

1 1 3 12 P₁ = 3*12*1 - (2*6*1 + 2*1) = (3*12 - (2*6 + 2))*1 = 22*1

2 1/2 3² 12*(1/2) P₂ = (3*22 - 6 - 6 - 1)*(1/2) = (3*22 - 13)*(1/2)

3 1/4 3³ 12*((1/2)²) P₃ = (3*(3*22 - 13) - 13)*(1/4) = (3*3*22 - 13*(1 + 3))*(1/4)

4 1/8 3⁴ 12*((1/2)³) P₄ = (3³*22 - 13*(1 + 3 + 3²))*(1/8)

... ... ... ... ...

n 1/2^n-1 3ⁿ 12*((1/2)^n-1) P_n = (3^n-1*22 - 13*(1 + 3 + 3² + ... + 3^n-2))*(1/2^n-1)

Total Perimeter vs level

Recognizing the bracketed sum in P_n is a finite geometric series, we see

P_n = (3^n-1*22 - 13*(1 + 3 + 3² + ... + 3^n-2))*(1/2^n-1)

= (3^n-1*22 - 13*(1 - 3^n-1)/(1 - 3))*(1/2^n-1)

= (3^n-1*(22 - (13/2)) + 13/2)*(1/2^n-1)

So P_n -> infinity as n -> infinity.

This suggests the limiting shape has infinite perimeter, yet some care is needed.

The perimeters of the cubes are longer than the perimeters of the corresponding pieces of the limiting shape, so we have just shown that infinity is an upper bound for the perimeter of the limiting shape.

More carefully, we see the limiting shape is a right isosceles gasket, which we have seen has infinite perimeter.

This is no surprise: the gasket has dimension Log(3)/Log(2) > 1, the perimeter is a 1-dimensional measure, and so the perimeter of a Log(3)/Log(2)-dimensional object is infinite.

Return to sample.