Cumulative Gasket Pictures

Exercise Solutions

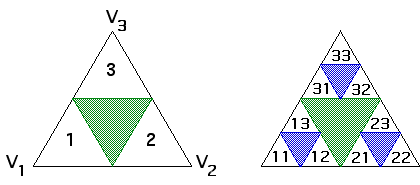
2. (ii) Suppose P1 lies in the largest removed triangle, hence inside the equilateral triangle S having vertices V1, V2, and V3.

Denote by T1, T2, and T3 the IFS rules equivalent to the rules of problem 1.

Then P2 = T1(P1), or P2 = T2(P1), or P2 = T3(P1), depending on the corner selected.

Consequently, P2 lies in one of the equilateral triangles T1(S), T2(S), and T3(S), labeled 1, 2, and 3 on the left above.

Say P2 = Ti(P1).

Note the three blue triangles on the right are T1, T2, and T3 of the green triangle, so P2 lies in one of the blue triangles.

Next, P3 = Tj(P2) = Tj(Ti(P1)), so P3 lies in one of the nine triangles 11 = T1(T1(S)), ..., 33 = T3(T3(S)) and so is not in one of the blue triangles.

All subsequent Pn = Tm(Tk( ... Tj(Ti(P1))...)) lie in Tm(Tk(S)) and so is not in one of the blue triangles.

Continuing in the obvious way shows each stage of removed triangles contains exactly one of the Pi.

Return to Exercises.