Data Analysis by Driven IFS

Sample

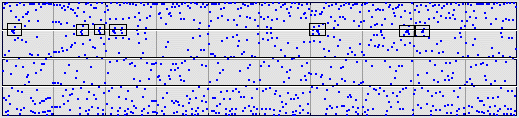
What about the clumps (outlined in boxes) along the bin 3 - bin 4 boundary?

To understand this, suppose we applied T3 and T4 infinitely many times in succession.

Suppose we start with the point (x0, y0) and begin applying T3 and T4 alternately. We'd get

T3(x0, y0) T4T3(x0, y0) T3T4T3(x0, y0) T4T3T4T3(x0, y0) T3T4T3T4T3(x0, y0) T4T3T4T3T4T3(x0, y0) T3T4T3T4T3T4T3(x0, y0) T4T3T4T3T4T3T4T3(x0, y0)

The left column converges to a point (x1, y1) having address 343434 ... = (34)infinity.

The right column to (x2, y2) having addess 434343 ... = (43)infinity.

What can we say about these points?

First, observe T₄(x₁, y₁) has address

4(34)^infinity = 4(34)(34)(34)(34)... = (43)(43)(43)... = (43)^infinity

That is, T₄(x₁, y₁) = (x₂, y₂).

A similar argument shows T₃(x₂, y₂) = (x₁, y₁).

Combining these observations, we see

T₃T₄(x₁, y₁) = (x₁, y₁) and T₄T₃(x₂, y₂) = (x₂, y₂)

The first of these gives the equations

(1/2)(x₁/2 + 1/2) = x₁ and (1/2)(y₁/2 + 1/2) + 1/2 = y₁

Consequently, (x₁, y₁) = (1/3, 1). Similarly, (x₂, y₂) = (2/3, 1).

If the alternation between T₃ and T₄ is repeated for a while, but not forever, the driven IFS should contain two sequences of points, one approaching (x₁, y₁), the other approaching (x₂, y₂). And indeed we do see this, indicated by the boxes in the diagram.

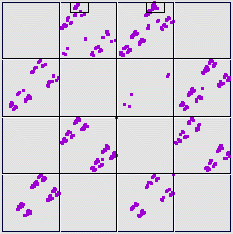Return to Equal-Size Bin Sample.