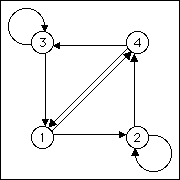
| Taking the fixed points at the ends of an edge of the square gives the
horizontal or vertical lines already studied. |
| The only other option is to take the fixed points at the ends of a
diagonal of the square. For example, suppose we take 3∞
and 2∞. |
| To obtain parallel lines we have two choices for the images of these fixed points: |
| 1(3)∞ and 4(2)∞ |
| As before, we look at the length 2 address squares through which the lines must pass. |
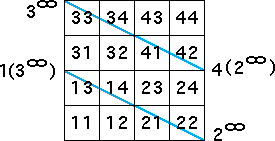 |
| and obtain |
| 3 → 3, 4 → 3, 1 → 4, 2 → 4,
3 → 1, 4 → 1, 1 → 2, and 2 → 2 |
| Here are the table, graph, and plot. Indeed, we obtain two lines. |
|
| Exercise 1 How many pairs of slanted lines can be generated in
this way? Try it first before consulting the
answers. |
| Exercise 2 Can either of these lines be generated independently of the
other? Try it first before consulting the
answer. |