Pascal's Triangle and Its Relatives

Exercises

Other mods

General Patterns

For prime n, the only clean fractal pattern occurs when the numbers 1, 2, ... , or n-1 (mod n) are shaded.

For composite n, say n = p*q for example, there are subgroups H1 isomorphic to Zp and H2 isomorphic to Zq.

Then there are isomorphisms

Zn/H1 -> Zq

Zn/H2 -> Zp

Shading the elements of Zn sent by the isomorphism to {1, 2, ..., q-1} in Zq gives the same fractal as shading the Pascal's triangle elements congruent to 1, 2, ..., or q-1 (mod q).

Now we generalize the observation that in the n -> infinity limit almost all binomial coefficients are even, that is, multiples of 2.

We deduced this by shading the odd numbers, those not multiples of 2, and noting this produced a gasket of dimension log(3)/log(2). Because dim < 2, almost all coefficients are multiples of 2. 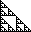Shading the numbers congruent to 1 or 2 (mod 3) produces a gasket of dimension log(6)/log(3). Consequently, almost all coefficients are multiples of 3. 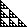Shading the numbers congruent to 1, 2, 3, or 4 (mod 5) produces a gasket of dimension log(15)/log(5). Consequently, almost all coefficients are multiples of 5. Shading the numbers congruent to 1, 2, 3, 4, 5, or 6 (mod 7) produces a gasket of dimension log(28)/log(7). Consequently, almost all coefficients are multiples of 7.

For every prime n, shading the numbers congruent to 1, 2, 3, ..., or n-1 (mod n) produces a gasket of dimension log(n(n+1)/2)/log(n) < 2.

log(n(n+1)/2)/log(n) n

Consequently, in the n -> infinity limit, almost all binomial coefficients are multiples of all prime numbers. Well, some care is needed in taking the limits.

Return to Other Mod Exercises.