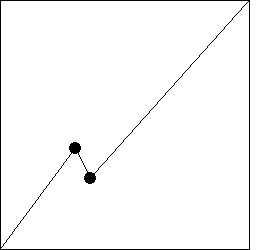
| For comparison, here is another example with dt1 = 0.3,
this time taking H = 0.75. |
| From the scaling condition we
see dt2 must satisfy |
| 0.30.75 - (dt2)0.75 +
(1 - 0.3 - dt2)0.75 = 1 |
| Mathematica can find dt2 using the
command |
| FindRoot[0.3^0.75 + x^0.75 + (1 - 0.3 - x)^0.75 == 1,{x,2}] |
| This gives |
| dt2 = x = 0.0598602 |
| Then from dt1 + dt2 + dt3 = 1, we obtain |
| dt3 = 1 - 0.3 - dt2 = 0.64014. |
| We calculate the
dYi from these by the unifractal scaling relation
|dYi| = (dti)H, and the up, down, up ordering of the
generator segments. |
| dY1 = 0.30.75 = 0.40536 |
| dY2 = -(0.05986020.75) = -0.121019, and |
| dY3 = (0.64014)0.75 = 0.715659. |
|
| The turning points are |
| (a, b) = (dt1, dY1) = (0.3, 0.40536), and |
| (c, d) = (dt1 + dt2, dY1 + dY2) = (0.3598602, 0.284341). |
|
| The generator is on the left; the 8th iterate, sampled at 3128 points, is on the right. |
|