Block Fractals

Exercises - Four Block Configuration Area

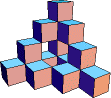
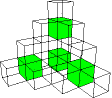
We estimate the area of the limiting shape by finding the area of each level of the construction, and taking the limit.

Click on the links A1 and A2 in Total Area of Squares for an explanation of how the areas are determined.

Interpreting the result will require some delicacy.

Level 1	Level 2

Level Side Length Number of Squares Square Area Total Area of Squares 1 1/2 4*6 - 6 (1/2)2 = 1/4 A1 = (4*6 - 6)*(1/4) = 6 - (6/4) 2 1/4 4*(4*6 - 6) - 6 = 42*6 - 6*(1 + 4) (1/4)2 A2 = (4*(4*6 - 6) - 6)*(1/4)2 = 6 - (6/42)*(1 + 4) 3 1/8 4*(4*(4*6 - 6) - 6) - 6 = 43*6 - 6*(1 + 4 + 42) (1/8)2 = (1/4)3 A3 = (4*(4*(4*6 - 6) - 6) - 6)*(1/4)3 = 6 - (6/43)*(1 + 4 + 42) ... ... ... ... ... n 1/2n 4n*6 - 6*(1 + 4 + ... + 4n-1) 1/4n An = 6 - (6/4n)*(1 + 4 + ... + 4n-1)

Total Area vs Level

Recognizing the bracketed sum in An as a finite geometric series with a1 = 1, and r = 4, we see

An = 6 - (6/4n)*((1 - 4n)/(1 - 4)

With some simplification we have

An = 4 + 1/(2*4n)

So An -> 4 as n -> infinity.

This is an upper bound for the area of the limiting shape. Unfortunately, we cannot conclude that the area of the limiting shape is 4, because of a well-known example.

Return to exercises.