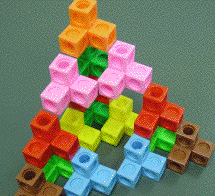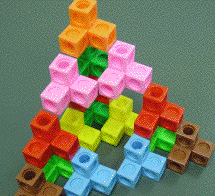| 1. (a) Build a model of the third stage of the four-block configuration. |
| (b) Compute the dimension of the limiting shape. From this, conjecture which measures are infinite and
which are zero. (Here is the answer.) |
| (c) Compute the perimeter of the limiting shape. If we expect the perimeter is infinite (from the dimension
results), we might simplify this computation by finding a family of perimeters contained in the perimeter of the corresponding
levels, and having an infinite limit. Perhaps one of the pervious perimeter computations will be useful.
(Here is the answer.) |
| (d) Compute the area of the limiting shape. (Here is the answer.) |
| (e) Compute the volume of the limiting shape. (Here is the answer.) |
| (f) Interpret these computations using the dimension. (Here is the answer.) |
| 2. (a) Build a model of the third stage of the five-block configuration. |
| (b) Compute the dimension of the limiting shape. From this, conjecture which measures are infinite and
which are zero. (Here is the answer.) |
| (c) Compute the perimeter of the limiting shape. If we expect the perimeter is infinite (from the dimension
results), we might simplify this computation by finding a family of perimeters contained in the perimeter of the corresponding
levels, and having an infinite limit. Perhaps one of the pervious perimeter computations will be useful.
(Here is the answer.) |
| (d) Compute the area of the limiting shape. If we expect the area is infinite (from the dimension
results), we might simplify this computation by finding a family of areas contained in the limiting shape
and having an infinite limit. (Here is the answer.) |
| (e) Compute the volume of the limiting shape. (Here is the answer.) |
| (f) Interpret these computations using the dimension. (Here is the answer.) |