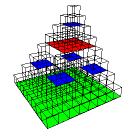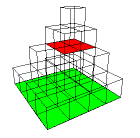
Block Fractals

Exercises - Five Block Configuration Area

We show the area of the limiting shape is infinite by finding a sequence of squares in the limiting shape, and showing the sum of the areas of these squares diverges.

Each stage of the construction contributes its own squares.

Level 1	Level 2	Level 3

Level Side Length Number of Squares Square Area Total Area of Squares 1 1 1 1 A1 = 1*1 2 1/2 1 (1/2)2 = 1/4 A2 = 1*1 + 1*(1/4) 3 1/4 5 (1/4)2 A3 = 1*1 + 1*(1/4) + 5*(1/4)2 4 1/8 52 (1/4)3 A4 = 1*1 + 1*(1/4) + 5*(1/4)2 + 52*(1/4)3 ... ... ... ... ... n 1/2n-1 5n-2 5n-2*(1/2n-1)2 = 5n-2*(1/4)n-1 An = 1 + ((1/4) + 5*(1/4)2 + 52*(1/4)3 + ... + 5n-2*(1/4)n-1)
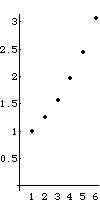Recognizing the bracketed sum in An as a finite geometric series with a1 = 1/4, and r = 5/4, we see An = 1 + ((1/4) - (5n-1/4n))/(1 - (5/4)) With some simplification we have An = 1 + ((5/4)n-1 - 1) = (5/4)n-1 Consequently, the limiting shape has infinite area.		Total Square Area vs level

Return to exercises.