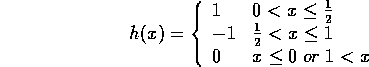
The Haar wavelet is defined as:
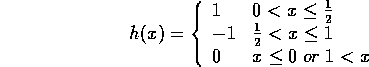
The Haar basis, consisting of the functions
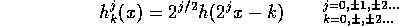
that is rescaled versions of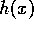 
(by 
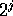) shifted by 
.
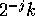These functions are orthogonal i.e.
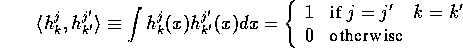
Moreover, they form a basis for all functions f with finite square integral
This means that we can represent such a function as
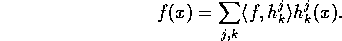
The coeffic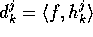ients 
are called the
Haar Wavelet coefficients.
In order to facilitate the transition between the functions (continuous) point of view and the discrete (sample) numerical approach we choose to discretize a function on a given scale by defining its ``sampled'' values as being averages on that scale, i.e. for a fixed j we define
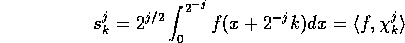
where
is called a scaling function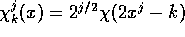 
(the
function is normalized so that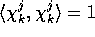 
).
The number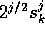 
is the average of f on the interval
.
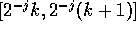We observe that 
, from
which we deduce the recursive algorithm for computing the Haar coefficients in
figure A.15.
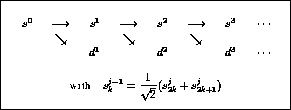
Figure A.15: Recursive algorithm for the Haar coefficients
Interpretation: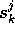 
represent the time average of the signal f
on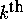 
time intervals of length 
, 
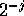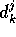represent the variation of the average time signal on two consecutive
intervals.