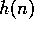We'll use the notation and terminology of [2], whose results we shall assume.
We are given an exact quadrature mirror filter
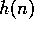satisfying the conditions of Theorem (3.6) in [2], p.
964, i.e.
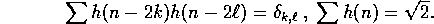
We let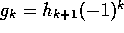 
and define the operations 
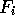on
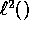into ``
''
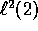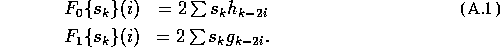
The map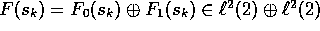 
is orthogonal and
We now define the following sequence of functions.
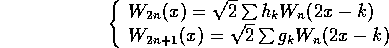
Clearly the function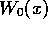 
can be identified with the function
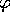in [D] and 
with the function 
.
Let us define 
and
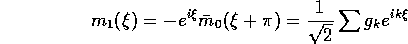
All of the functions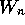 
have a fixed
scale, but
we observe that mixed-scale decompositions of 
are also possible.
This allows us to refine the decomposition 
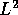by
scales
as embodied in the following:
