 as the dyadic subinterval
as the dyadic subinterval
 of
of 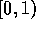 . Such an indexing convention
gives a
faithful correspondence between disjoint dyadic decompositions of
the frequency line
and orthonormal wavelet packet subsets of
. Such an indexing convention
gives a
faithful correspondence between disjoint dyadic decompositions of
the frequency line
and orthonormal wavelet packet subsets of  .
.
We may also think of  as the dyadic subinterval
as the dyadic subinterval
 of
of 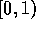 . Such an indexing convention
gives a
faithful correspondence between disjoint dyadic decompositions of
the frequency line
and orthonormal wavelet packet subsets of
. Such an indexing convention
gives a
faithful correspondence between disjoint dyadic decompositions of
the frequency line
and orthonormal wavelet packet subsets of  .
.
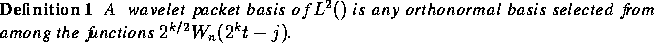
Beside the Walsh-type basis , examples of wavelet packet bases include the wavelet basis and the subband basis
A useful picture of the tree of wavelet packet coefficients is that of a rectangle of dyadic blocks. The row number within the rectangle indexes the scale of the wavelet packets listed therein. The column number indexes both the frequency and position parameters. We may choose to group the wavelet packets either by position or by frequency. Grouping by position fills each row of the rectangle with adjacent windowed spectral transforms, analogous to windowed FFT, with the window size determined by the row number and the window position corresponding to the location of the group. The frequency parameter increases within the group.
We will group the coefficients by frequency, since that gives a
more efficient implementation, and since the transformation to the
other form is obvious. The boxes of coefficients in the rectangle
correspond to the decomposition of  into the
subspaces
into the
subspaces  , for
, for 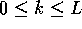 and
and  . The top box corresponds to
. The top box corresponds to 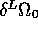 , the
bottom boxes correspond to
, the
bottom boxes correspond to 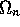 , for
, for 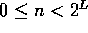 , and box
n on level k (counting the bottom as level 0) corresponds to
subspace
, and box
n on level k (counting the bottom as level 0) corresponds to
subspace  .
.
For definiteness we recall the Haar example. Consider a function defined at 8
points 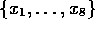 , i.e., a vector in
, i.e., a vector in  . Then the (periodized)
wavelet packet coefficients of this function look like figure A.18.
. Then the (periodized)
wavelet packet coefficients of this function look like figure A.18.

Figure A.18: A rectangle of wavelet packet coefficients.
Each row is computed from the row above it by one application of
either 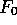 or
or 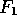 , which we think of as ``summing'' (
, which we think of as ``summing'' ( ) or ``differencing''
(
) or ``differencing''
(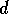 ) operations, respectively. Thus, for example, the subblock
) operations, respectively. Thus, for example, the subblock
 comes from the application of
comes from the application of 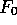 to
to
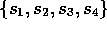 ,
while
,
while 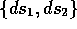 comes similarly from
comes similarly from  . The two descendent
s and
d subblocks on row n+1 are determined by their mutual parent on
row n,
which conversely is determined by them through the adjoint
anticonvolutions
. The two descendent
s and
d subblocks on row n+1 are determined by their mutual parent on
row n,
which conversely is determined by them through the adjoint
anticonvolutions
 and
and  .
.
The algorithm produces Haar wavelet packets in the ``Paley'' or
``natural''
order. The algorithm may be easily modified to produce ``sequency''
ordered
wavelet packets: what is needed is to exchange 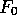 and
and 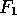 whenever the
parent's sequency is odd.
whenever the
parent's sequency is odd.
Sequency has a strict definition only for Walsh functions, where it is the
number of zero-crossing of a function which takes only the values 1 and
-1. The nth Shannon wavelet packet, in sequency order, is band-limited to
the intervals  . If we define the appropriate notion of ``main
frequency'' in the intermediate case of smooth, compactly supported wavelet
packets, we see that main frequency increases monotonically with sequency
order.
. If we define the appropriate notion of ``main
frequency'' in the intermediate case of smooth, compactly supported wavelet
packets, we see that main frequency increases monotonically with sequency
order.
Paley order can also be obtained from sequency order by the Gray code permutation.