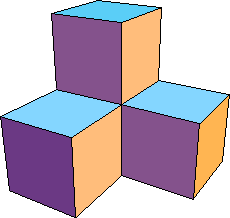
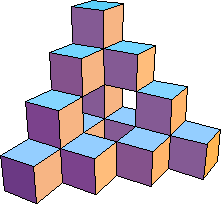
| Comapring the first (left) and second (right) levels of the construction, we see the
limiting shape is made of 4 copies of itself, each scaled by a factor of 1/2. |
| Recall the similarity dimension formula:
a shape consisting of N copies of itself,
each scaled by a factor of r, has dimension |
| d = Log(N)/Log(1/r) |
| Consequently, the limiting shape of the four block configuration has dimension |
| d = Log(4)/Log(2) = Log(22)/Log(2) = (2*log(2))/Log(2) = 2. |
| From our study of the gasket, we expect |
the perimeter of the limiting shape is infinite, |
the area of the limiting shape is ... hmmm, it might be anything, and |
the volume of the limiting shape is 0. |
| Let's see how our calculations agree with these conjectures. |